主要用于获取 特定的参数,使得损失函数变得最小。
- 损失函数:
$$
J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}-y^{(i)})^2
$$
迭代过程
下图显示梯度下降的过程
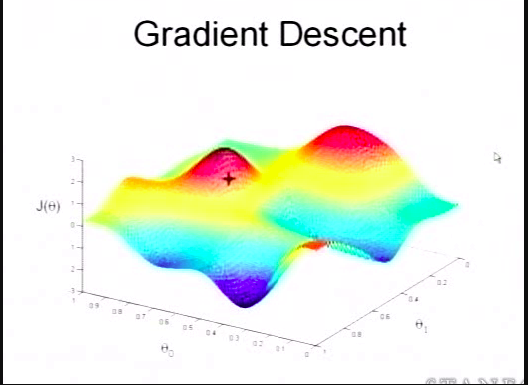
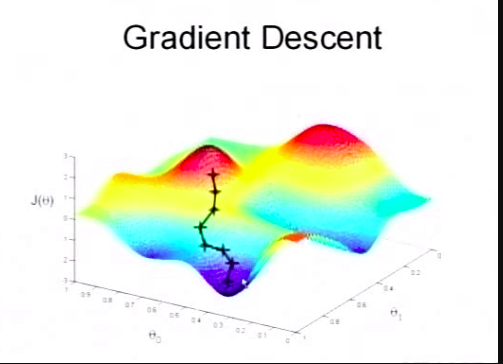
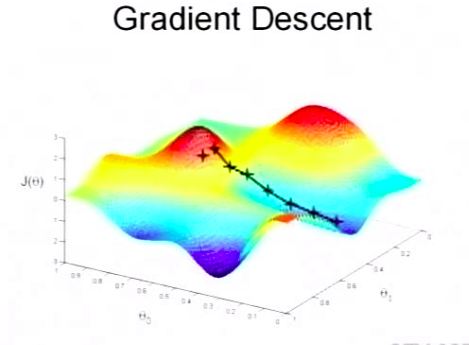
更新函数:
$$
$\theta_j:=\theta_j-\alpha\frac{\partial}{\partial \theta_j}J(\theta) $
$$
其中 $\alpha$ 表示学习速率,$\alpha$ 过大会导致错失最小值,$\alpha$ 过小会导致更新速度变慢
简化偏导
$$
\frac{\partial}{\partial \theta_j}J(\theta) = \frac{\partial}{\partial \theta_j}\frac{1}{2}(h_{\theta}(x)-y)^2
=2\frac{1}{2}(h_{\theta}(x)-y) \frac{\partial}{\partial \theta_j}(h_{\theta}(x)-y)
=(h_{\theta}(x)-y)* \frac{\partial}{\partial \theta_j}(\sum_{i=1}^{n}\theta_{i}x_{i}-y)
=(h_{\theta}(x)-y)* x_{j}
$$
单训练样本更新函数
$$\theta_j:=\theta_j+\alpha(y^{(i)}-h_{\theta}(x^{(i)})) x^{(i)}_{j}$$
多训练样本更新函数
$$\theta_j:=\theta_j+\alpha\sum_{i=1}^{m}(y^{(i)}-h_{\theta}(x^{(i)})) x^{(i)}_{j}$$